什麼是 B-tree?
B-tree 是一種資料結構,其節點所儲存資料是有序的,如下圖所示,每一個節點所包含的值是以遞增的方式排序。其內部節點擁有可變數量的 key,且 key 左邊的值小於自己;右邊的值大於自己。

B-tree 並不是唸作
B減樹,不要因為把它跟 B+tree 拿來做比較,就自動把它唸成B減樹摟!
為何需要 B-tree?
在資料庫的索引 Index,便是使用 B-tree 當作資料結構,那為何不能使用其他資料結構呢?
想想看要如何搜尋一筆資料,最直觀的作法便是從第一筆資料到最後一筆資料,去搜尋相符的資料即可,其時間複雜度為 O(n)。但這種作法,在資料量龐大時的效率明顯不佳,如果運氣好的話可以在前幾筆就找到想要的資料,否則也有可能資料出現在最後一筆,要加強搜尋的效率,接著想到的方法便是二元搜尋 Binary Search,使用這種資料結構能將搜尋資料的複雜度降低至 O(log n)。
接著我們回頭看,B-tree 搜尋資料的時間複雜度其實也是 O(log n),跟二元搜尋的時間複雜度相比,其實是一樣的,那為什麼我們不採用 Binary Search,而是要使用 B-tree? 這就牽扯到硬碟IO的議題了。
今天之所以會使用到索引,就是因為資料量龐大,想要增加搜尋的效率而使用。資料量龐大導致索引的資料也相對的龐大,這麼多的資料並不會儲存在記憶體,而是在硬碟裡,既然儲存在印碟裡,就如同前面所說,會牽涉到IO的問題。
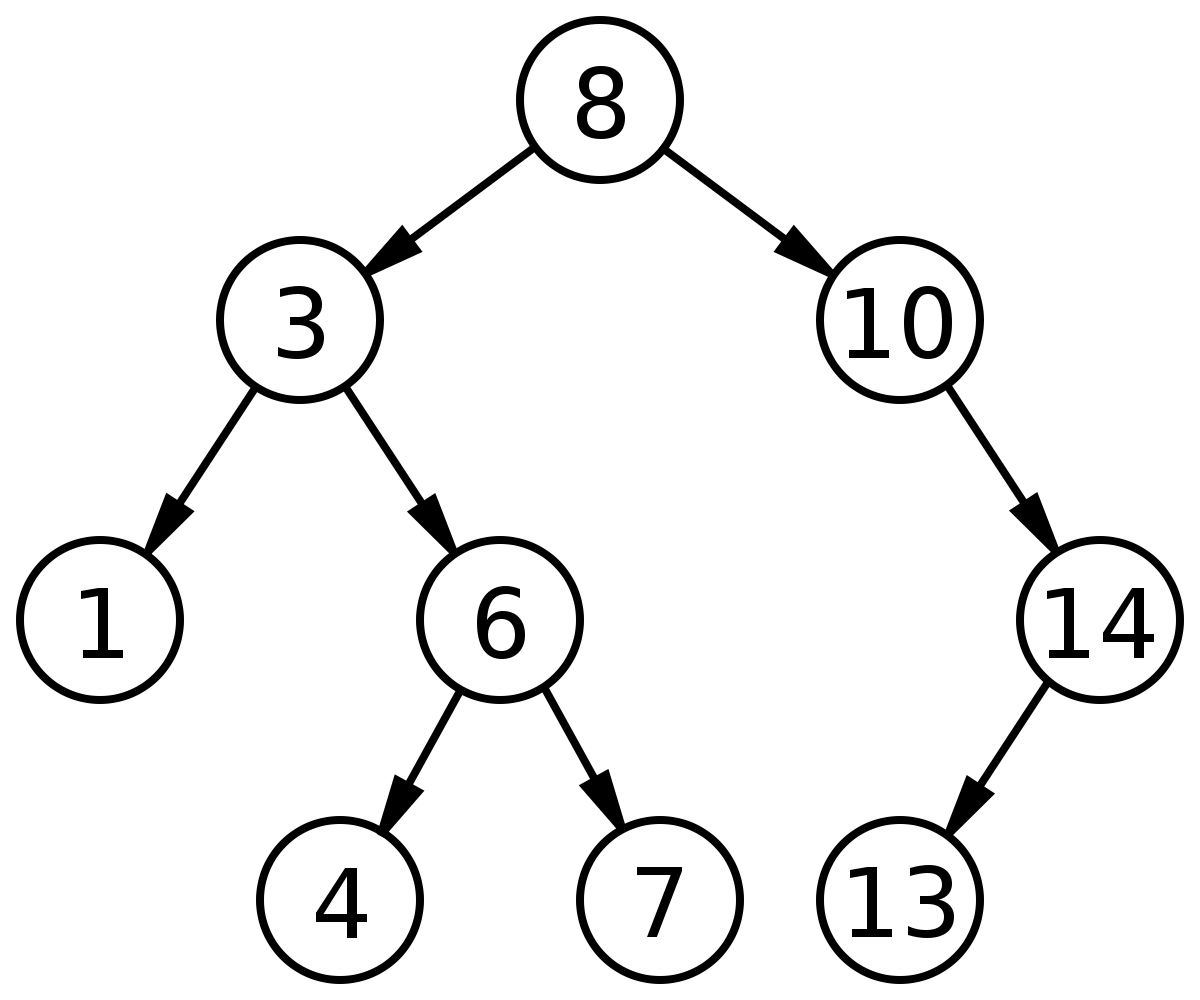
因為計算資料都要在記憶體上進行,透過索引搜尋資料且索引很大時,並不能一次將索引放進記憶體,而是會將資料逐一放進記憶體。假設二元搜尋樹的結構如下圖,每一個節點代表一個索引,搜尋的順序便是 8 -> 3 -> 6 -> 7,聰明如你便可以想像得到,如果今天要搜尋到 7,因為資料結構的關係,導致使用了 Binary Search Tree 的索引總共要進行 4次 的硬碟 IO。
若是使用 B-tree 的資料結構實作索引,如下圖,若是我們要找 117,我們只要進行 3次IO,雖然每一個節點要比較的元素變多了,但因為這些元素都已經放進記憶體,在記憶體進行比較的耗時幾乎可以忽略。相同的資料若是使用二元搜尋樹,樹會變得很高,樹越高,IO 存取的次數也就越多。

整體的重點就是: 降低硬碟 IO 的存取次數,才是一個適合索引的資料結構
抑或是說,比起又高又瘦的樹狀結構,又矮又胖的樹狀結構反而更適合當作索引的資料結構。